notions of heat exchange

Conduction is heat transported between two bodies in contact that are at different temperatures or between two parts of the same body that are at different temperatures.

The heat flow Ø transmitted by conduction over a length x across an area S perpendicu­lar to this flow is given by the Fourier law :

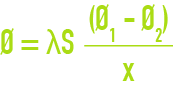
θ₁ – θ₂ representing the drop in temperature over the distance x, λ being the heat conduction coefficient for the material expressed in practice in W·m^–1 by °Kelvin.

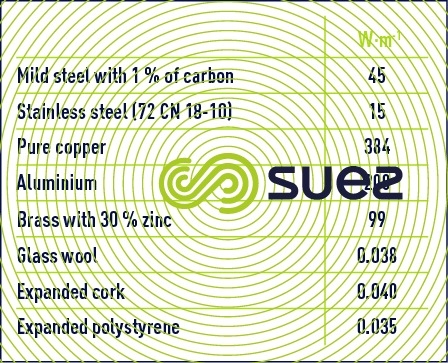
For most solids, λ is an almost linear function of the temperature: a λ = λ (1 + aθ); l is usually positive for insulators and negative for metals except aluminium and brass. However, heat conduction coefficient variation based on temperature is relatively low. Between 0 and 100 °C, the following values can be used as an initial approximation (table 88) :

Click here to create your account in order to view the illustrations

At ambient temperature, the following values can be used :

• still water = 0.58 W·m^–1;
• calm air = 0.027 W·m^–1·K^–1.

The Fourier equation can also be written as follows :

With regard to conduction through several materials in series, for a total temperature drop Δθ, we can write :

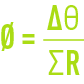
Convection is heat transferred in a fluid from a solid under the effect of motion that is caused by density differentials (natural convection) or that is mechanically induced (forced convection).

In practice, heat transfer from a solid body at temperature θ and a fluid at temperature θ₁ involves both the convection and the conduction processes, making this a particularly complex phenomenon. We can then establish a global transmission coefficient k such that :

Using the same system of units, the value of k depends on certain physical properties of the fluid, on its circulation velocity, on the geometry of the solid. This means that the values for k can vary widely. For example, the following values are feasible (table 89) :

Click here to create your account in order to view the illustrations

For additional information, our readers might find the following of use :

• the Aide-mémoire du thermicien (see heat transfer) publ. Elsevier;
• the Techniques de l’Ingénieur (see energy engineering) vol. BE₁.

Radiation is the transmission of heat as radiated energy. This phenomenon takes place without material support and, therefore, can take place in a vacuum.

The Stefan-Boltzmann law provides the heat flow emitted by radiation :

T being the absolute temperature of the radiant body, e an emission factor equal to 0 for a perfect reflector and to 1 for a black body and k being a dimensional constant.

heat exchangers

The quantity of heat passing through a wall can be written as follows :

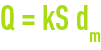
• S is the exchange surface area in m^2;
• d_m is the mean temperature difference between the two sides of the wall, characterised by the logarithmic mean of fluid incoming and discharge temperatures;
• k is the global transmission coefficient in W·m^–2·K^–1 or in mth·m^–2·h^–1. °C according to the nature and conditions applicable to fluid flow and to wall characteristics
• Q is expressed in watts or in mth·h^–1 depending on the system of units selected.

In the case of complex media such as sludge, the transfer coefficient will be mainly experimental. For example, through tube heat exchangers :

• in sludge digestion, the exchange coefficient can reach values of up to 1,300 W·m^–2·K^–1 [1,100 mth·m^–2·h^–1 °C] for fluid velocities of between 1 and 2 m · s^–1;
• in sludge heat treatment, with sludge-sludge exchangers, the exchange coefficient can reach 350 W·m^–2·K^–1 [300 mth·m^–2·h^–1 °C] for fluid velocities of up to between 0.5 and 1 m·s^–1.

determination of the logarithmic mean of temperatures

Let us assume a backflow heat exchanger within which two fluids are circulating.

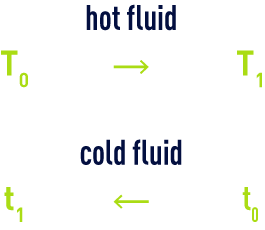
The logarithmic mean is provided by the following relation :

Click here to create your account in order to view the illustrations

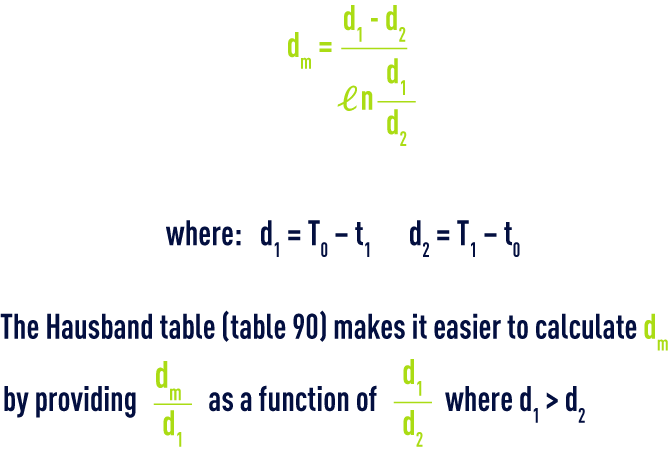
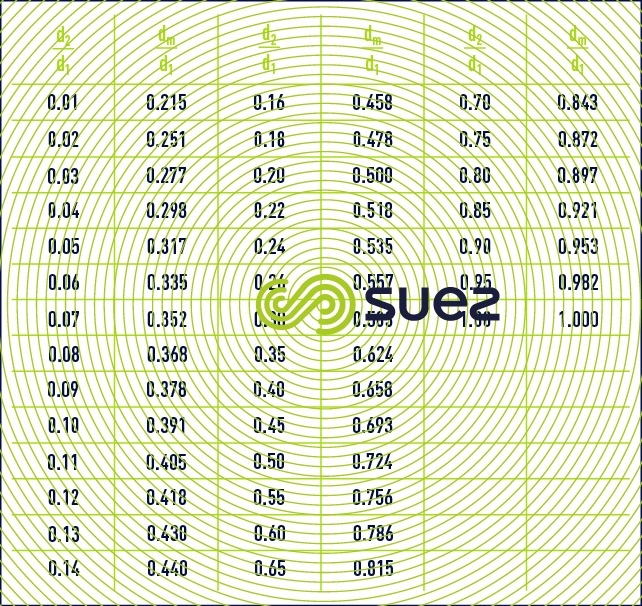
Note : mathematically, it can be demonstraded that if

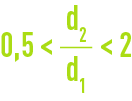
, the difference between the logarithmic mean and the arithmetical mean is less than 5 %. This comment justifies the fact that the arithmetical mean is often used in most exchangers used in sludge treatment applications.