weirs
Reading time:Weir discharge is provided by the general formula:


where :
Q = flow rate, in m3·s–1 (or L·s–1),
μ = weir discharge coefficient,
Ls = weir crest width, in m,
h = water sheet height, in m (or cm),
g = gravity acceleration in m·s–2, (9.81 in Paris).
Additionally, P is used for the «height of the weir crest above the upstream channel» and L for the canal width upstream from the weir.
thin-walled rectangular weir with a low approach velocity


in the case of a reservoir outlet for instance.
special case of a circular overflow weir
for an overflow having a diameter of 0.20 m < Ø < 0.70 m with enough nappe fall to avoid any downstream reaction.


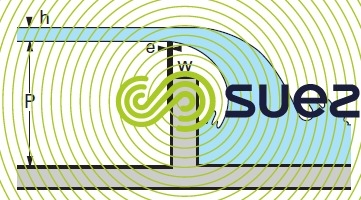
thin-walled rectangular weir on a channel
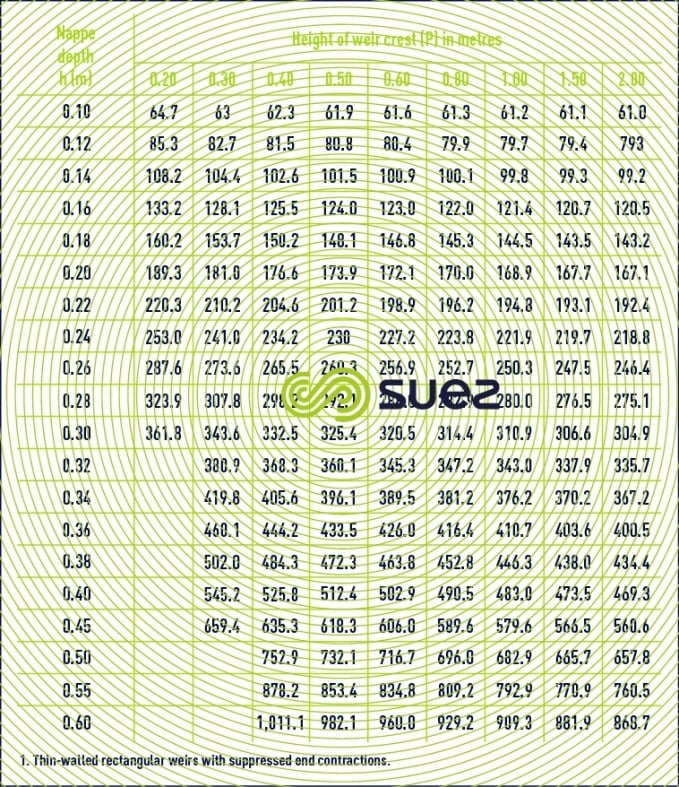
weir with suppressed and contractions (Ls = L), with free nappe flow (figure 43)
This definition applies to a weir when the crest thickness e is less than half of load h, when flow is such that, at atmospheric pressure, it leaves an air-filled space between the water sheet and the crest’s downstream wall, and when the overflow blade width is exactly the same as that of the channel.


The flow rate coefficient µ is provided by one of the following formulae :
- Bazin formula (1898), generally used in France :

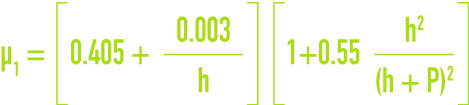
- Formula suggested by the Société des Ingénieurs et Architectes Suisses (Society of Swiss Engineers and Architects - SIA):


These formulae, where h and P are expressed in m, can be used for heads on the weir crest h of between 0.10 and 0.60 m 9 in the case of the Bazin formula, and between 0.025 m and 0.80 m in the case of the SIA formula, the latter providing slightly inferior results to those of the Bazin formula.
The following conditions need to be verified:
- for Bazin: P between 0.20 et 2 m.
- for SIA: P greater than h.
Finally, h must be measured at a threshold distance equal to at least five times the maximum head on the weir crest. When there is not enough aeration below the nappe (depressed nappe), the flow rate increases and its law becomes poorly defined; this is not acceptable for a measuring weir.
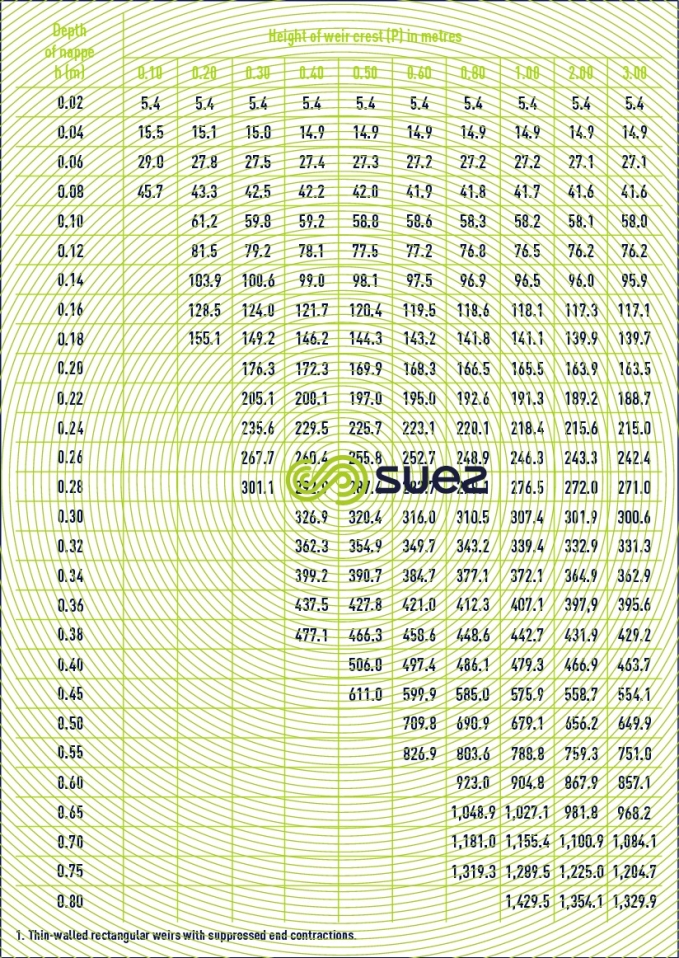
end contraction weir
The SIA puts forward the following formula for µ :

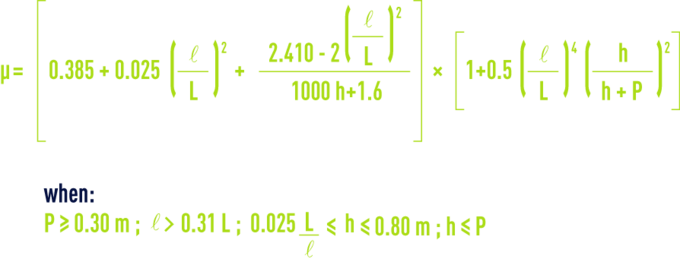
The simplified Francis formula should also be noted :

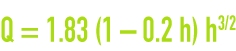
where the excress width on either side of the crest must be equal to at least 3 h, the height measured at least 2 m upstream from the weir crest.




thin-walled tringular weir

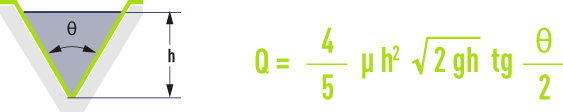
where :
Q = flow rate, in m3·s–1,
μ = Bazin flow rate coefficient for a thin wall, rectangular weir with suppressed end concentrations,
h = height on the weir crest, in m,
θ =angle at the weir apex.
The flow rate for a triangular weir can be deduced from the flow rate for a rectangular weir with suppressed end contractions, for the same height on the weir crest and the same height of weir crest above floor of channel, multiplying this flow rate by:

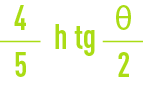
For θ = 90°, the Thomson formula is sometimes used:

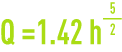
This is a very approximate formula because it does not allow for the effect of the height of the weir crest above the floor of the channel.
Bookmark tool
Click on the bookmark tool, highlight the last read paragraph to continue your reading later












