ozone transfer

The ozone produced is a gas, diluted in air or oxygen. Ozone is mainly used in its dissolved form so that it reacts according to the reactions described in the oxidants and disinfectants. Therefore, reactivity is governed by the amount of ozone transferred in the aqueous phase. The ozone first has to diffuse in the gas phase towards the gas-liquid interface before dissolving in the liquid and then it has to diffuse within the liquid itself.

The transfer rate will depend on :

• the physical properties of both phases present;
• the difference in concentration on either side of the interface together with the rate of chemical reaction consuming the ozone;
• the level of turbulence in the medium.

modelling the ozone transfer

The general transfer equation is written as follows :

Several models, based on different liquid behavor hypotheses, can be used to simulate ozone transfer in the aqueous phase. Accordingly there are the twin film model, the surface replacement models, the penetration models, combined models…

The simplest and most widely used model is the Lewis and Whitman twin film model (figure 13).

Click here to create your account in order to view the illustrations

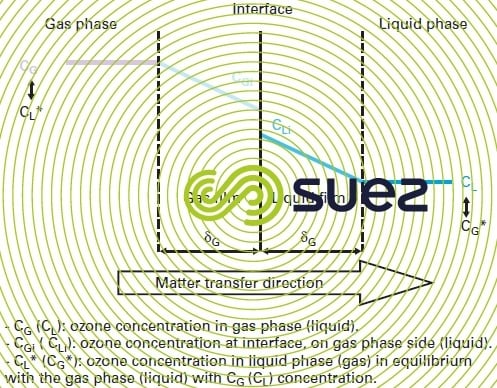
This model is based on the following assumptions :

• there is an interface between the gas and liquid phase that has no thickness;
• on either side of the interface separating the two phases, the resistance to the transfer lay in a gas film (δ_G thick) and in a liquid film (δ_L thick); each has its own transfer coefficient;
• the phases are in equilibrium at the interface and the concentrations obey the Henry law: C_Gi = m · CL_i where m is the partition coefficient linked to the Henry constant;
• outside the two films, an even concentration exists within each phase;
• passage through the two films takes place continuously.

The quantity transferred per unit of time N through the interface (excluding chemical reactions) can then be described by :

where: k_G and k_L (K_G and K_L) are the (overall) matter transfer coefficients within each phase and A, the interface exchange surface area.

As ozone is slightly soluble in water, resistance to mass transfer is located in the liquid film and, therefore

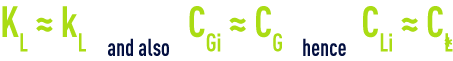
and if A is expressed as a function of the exchange surface area a per liquid phase unit of volume, the transfer equation reveals the product k_L · a called global mass transfer parameter :

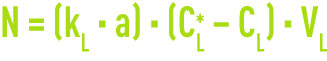
This latter equation is the basis used for estimating the matter transfer rate when considering any matter exchanger whatsoever (absorber or contactor). In order to apply this in practice, we need to know all these parameters:

• k_L · a: depends on the liquid phase’s hydrodynamic conditions;
• C_L: depends on agitation conditions and on the rate of the chemical reaction;
• C_L^*: in the saturated liquid phase, this concentration depends on the gas phase concentration, on temperature, pressure and the composition of the liquid phase.

ozone saturation concentration

The ozone concentration C_L* at saturation represents the dissolved ozone concentration in equilibrium with the gas phase concentration for a given temperature and pressure in the absence of a reaction. It is mistakenly termed solubility whereas, in the strictest sense, gas solubility is defined precisely as the concentration of dissolved gas in equilibrium under normal temperature and pressure conditions (0 °C and 1 atm). As ozone is not very soluble in water, the equilibrium obeys the HENRY law: x · He = y · P where x(y) is the molar fraction of the ozone in liquid phase (gas), P the gas pressure and He the Henry constant. If we assume that ozone is an ideal gas that produces diluted aqueous solutions (x < 0.05), the usual partition coefficient m also known as the solubility ratio and written α and defined as the ratio of the concentrations expressed in the same unit (g or mol ·m^–3), C_L* = m ·C_G is, therefore, linked to the Henry constant by :

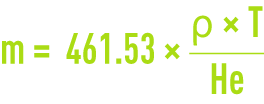
where ρ is the water density (in kg·m³) at a temperature T (in K) and He in Pa for P = 1 atm or 101.325 kPa.

It appears that He, ρ and therefore, m vary with the temperature. The data collected from the most recent studies can be trended by the following empirical law:

where T is expressed in °C and P = 1 atm.

The various equations reveal that three physical parameters have a major effect on the ozone concentration equilibrium in the gas and the liquid phases:

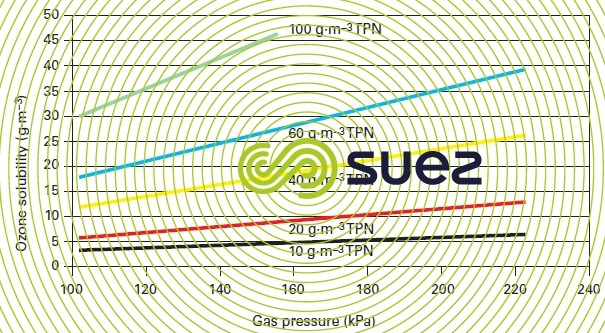
• increasing gas pressure or an increasing ozone concentration in the gas phase result in a linear increase of the dissolved ozone concentration at saturation for a given temperature
  (figure 14).
• conversely, the dissolved ozone concentration at saturation decreases as temperature rises (figure 36, characteristic constants of gases) while all other parameters remain unchanged.

Click here to create your account in order to view the illustrations

In practice, other parameters impact the equilibrium. The most important of these parameters are the pH and the ionic strength:

• the pH affects the rate at which ozone breaks down. The impact of an increasing pH becomes quite noticeable from a pH value above 8, which results in a reduction of the ozone concentration in equilibrium (see figure 37, characteristic constants of gases). Accordingly, experimental data converges towards the expression of an apparent Henry constant:

where the apparent He is given in atm, the temperature T in K and [OH^–] in mol · L^–1.

• the impact of the ionic force on dissolved ozone concentration at equilibrium becomes significant when the dissolved mineral content exceeds 1,000 mg · L^–1.