floatability and rising velocity
Reading time:general, terminology
Unlike sedimentation, flotation is a solid-liquid or liquid-liquid separation process applied to aggregates that have a lower density than the liquid containing them; these aggregates are finally collected as scum (floated sludge) from the surface of the units.
Flotation is termed natural when the density differential between the aggregates and the water is naturally sufficient for separation to take place.
Flotation is termed aided when it uses outside assistance (gas, air, nitrogen or natural gas and eventually with reagents) to enhance the separation of particles that are naturally floatable (but having an inadequate separation rate).
Flotation is said to be induced when the particle’s density, originally greater than that of the liquid, is artificially reduced in order to ensure its flotation. This process takes advantage of the capacity of some solid (or liquid) particles for uniting with gas bubbles (usually air or nitrogen) in order to form "particle-gas" pairs that are less dense than the liquid of which they constitute the dispersed phase. Consequently, the phenomenon applied is a triphasic one (gas-liquid-solid) and will depend on the physical-chemical properties of the three phases and especially on the affinity existing between their interfaces (more or less hydrophobic).
Typical terminology refers to average bubbles measuring 2 to 4 mm, fine bubbles a few µm to 1 mm and, finally, microbubbles from 40 to 70 μm.
In the water treatment field, it is customary to use the term of flotation (in the strict sense) exclusively for flotation induced by using microbubbles similar to those found in "white water" delivered by a tap on a water main rich in gas dissolved under high pressure. This process is called dissolved gas flotation ( DAF ).
However, in minerallurgy and in the oil industry, when air or any other gas is dispersed and produce fine bubbles measuring 0.2 to 2 mm in diameter, this is termed induced air flotation ( IAF ) or induced gas floatation ( IGF ).
relationship between design and bubble velocity
A gas microbubble’s rising velocity through water in laminar operating conditions can be calculated using the Stokes equation (see different types of sedimentation) :

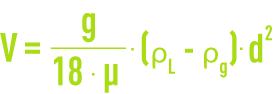
where
g = gravity acceleration
d = bubble diameter,
ρg = gas density,
ρL = liquid density,
μ = dynamic viscosity.
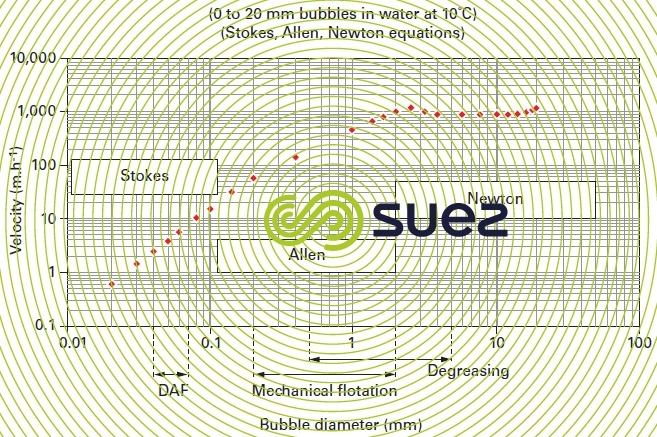
As the bubble diameter increases, its increasing rising velocity augments the flow turbulence around the bubble and Stokes law ceases to apply; therefore figure 31 makes successive use of the Stokes, Allen and Newton (see different types of sedimentation) equations to calculate the rising velocity of bubbles measuring between 20 and 20 000 μm.
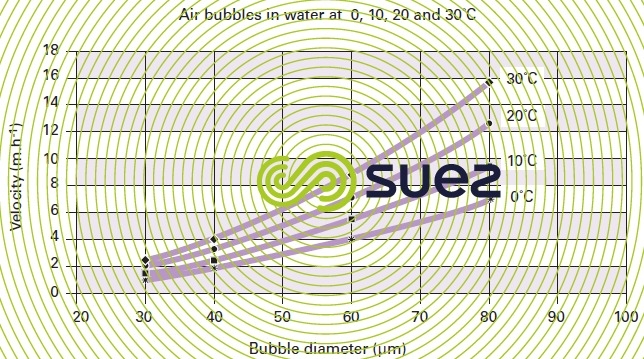
Thus we find that (figures 31 and 32) :
- 50 μm bubbles have a rising velocity of approximately 6 m · h–1 to 30 °C or 4 m · h–1 to 10 °C;
- whereas the rising velocity of bubbles that have diameters of approximately 1 mm is approximately 100 times higher.




particle-bubble composite
rising velocity
The Stokes equation continues to apply when:
- d is the particle-bubble "composite" and when g is replaced by ρa = particle-bubble "composite" density which directly depends on the gas volume/composite volume ratio;
- allowance is also made for the "gas bubble-particle" shape or sphericity.
bubble size considerations
The use of microbubbles is required for floc separation; in effect, there is 8,000 times more gas in a 1.2 mm bubble than in a 60 μm microbubble; therefore:
- if we want a good distribution of bubbles over the entire section of the unit, using bubbles of a few millimetres in diameter would result in a gas flow rate that is much higher than the one applied with microbubbles, and this large quantity of gas would create extremely disruptive turbulent currents.
- the increased bubble concentration increases the probability of collision between solid particles and bubbles. Furthermore, the low microbubble rising velocity compared with the fluid mass, means that microbubbles will adhere well to the fragile particles that make up the floc;
- finally, bonding will be easier if the microbubble diameter is lower than that of the suspended floc.
Larger bubbles (fine or even medium bubbles will do) can be used to separate out voluminous particles that are lighter than water, hydrophobic and that float naturally and where we only seek to enhance their floatation and to maintain the «cake» on the surface. This applies to fats separation.
minimum volume of gas required to ensure floatation
The minimum volume of gas Vg, having a density of ρg, required to ensure the floatation of a particle having a volume Vs and a density ρs in a liquid having a density ρL, can be calculated using the following equation:

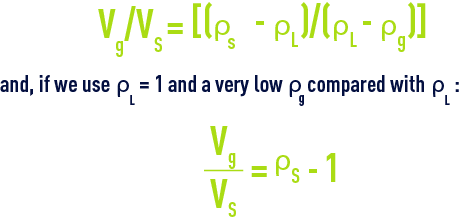
thus, a few percent (0.5 to 2%); in fact, we normally use 4 to 6% of gas in relation to the volume of floc in order to ensure that the composite rises “rapidly” or even more in drinking water flotation units.
importance of floc quality
As the microbubbles are between 10 and 100 times larger than the colloids, their collision is negligible and their coagulation-flocculation constitutes an essential pre-condition to their flotation (and to their settling).
Additionally, the microbubble/floc mixing zone is always turbulent and therefore, floc must be sufficiently strong to withstand shear forces.
With regard to biological floc, the quality of the bio flocculation also has an undeniable effect on its flotation performances (hydration, Mohlman index, floc size …). In particular, bulking activated sludge (containing filamentous bacteria) are the most difficult to float.
Bookmark tool
Click on the bookmark tool, highlight the last read paragraph to continue your reading later












