fundamental equations
Reading time:in-depth filtration
head loss
As it percolates through a granular filter bed, water loses energy, i.e. pressure, through friction which is designated head loss. At low velocities (laminar flow conditions), this head loss is governed by Darcy’s equation:


where V: filtration velocity,
K: filtering layer permeability,
ΔP: head loss through the filtering layer,
H: depth of the layer concerned,
μ: dynamic viscosity of the water,
R filtering layer’s filtration resistance,
Head loss ΔP will be proportional to filtration rate V, to the dynamic viscosity of the water, to the depth of the layer and inversely proportional to the filtering medium’s permeability (or directly proportional to this medium’s resistance).
The Kozeny (or Kozeny-Carman) formula quotes Darcy’s equation by clarifying the impact made by the porosity of the filtering medium on the specific surface area of the granules :

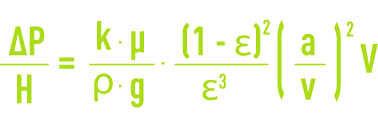
where, in addition to the above definitions:
k: Kozeny’s constant (approximately 5),
ρ: fluid’s density,
g: gravity acceleration,
ε: porosity of the filtering medium,
a/v: specific surface area per unit of volume of diameter d filtering granules, i.e. 6/d for a spherical granule.
For higher velocities, in upflow or downflow mode (e.g. wash mode or approaching fluidisation), we move into a transient or turbulent mode. We then have to apply Ergun’s formula which is based on Kozeny’s formula, modifying k and adding a correction term to k, representing the kinetic loss of energy through the medium:

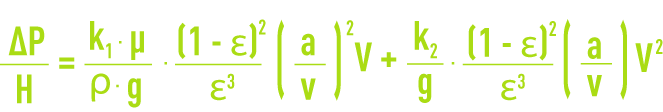
where k1 = 4.17,
k2 = 0.3 (round grains) to 0.48 (crushed grain).
Ergun’s formula is more general because it applies to all hydraulic conditions. In the case of high velocities, the second term which is proportional to the square of the velocity, becomes preponderant.
Empirical correlations have been established. For example, the following correlation applies to round grain sand within the 0.5 to 1.5 mm granulometry range :


where ES: effective size of the sand (see section material properties),
μt: dynamic viscosity of the water at t °C.
Exponent 1.20 affecting velocity translates the fact that flow is no longer perfectly laminar at typical velocities.
influence of fouling
The above formulas apply to a clean and homogenous medium (R constant throughout the depth). However, as a liquid containing suspended solids percolates through this medium, and as these suspended solids are gradually captured, this has an impact on the properties of the medium, especially its porosity e which decreases and head loss that increases according to an empirical law of the following type:


where σ: specific deposit (volume of deposit per unit of filter bed volume),
a: experimental coefficient.
Fouling is evenly distributed throughout the filter (the upper layers retain a greater proportion of particles) and the different coefficients can have very different values depending on the nature of the solids to be screened out and whether or not these solids have been coagulated. Therefore, experimentation is essential and the above laws can then be used to interpolate or extrapolate the results obtained.
minimum fluidization rate
In upflow conditions, we can write that the minimum fluidisation rate (Vmf) (see fluidisation) is reached when the head loss is equal to the apparent weight of the bed per unit of surface area (real weight less the Archimedes thrust) :

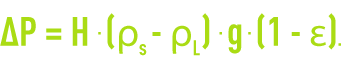
There are also empirical equations (Leva, Moll) used to calculate this velocity. Table 37 (see fluidisation) provides Vmf values common filtering media.
filtration of a loaded liquid accompanied by the formation of a cake
In this case, we will consider filtration ‘through a support’ of a solids-laden liquid accompanied by the formation of a cake of increasing thickness. This is the case of sludge treatment (pressurised sludge filtration using a belt filter or a belt pressure filter).
In the Darcy law expression, we can then accept that R includes both resistances in series, on the one hand the cake’s resistance Rg and, on the other, the filter belt’s initial resistance Rm.
The formulation of the equation is further expanded on in section filters. Please also refer to the section filtrability test for laboratory testing protocols used to measure R and the compressibility coefficient.
A similar approach can be used for filtration systems using filter belts or cartridges.
Bookmark tool
Click on the bookmark tool, highlight the last read paragraph to continue your reading later












